The 40% Rule (or why you don't draw that FoW)

If you've been reading legacy forums, you're bound to come across the saying that you'll have a Force of Will in your opening hand 40% of the time. This article will explain the trinkets behind the magic number 40. You'll also learn how to build a better manabase by finding out how many lands is enough.

And relax, there's not much math involved. If you know how to count from 1 to 60 and know how to multiply using a calculator, you'll be able to get through this easily.

A Narrative Walk through Probability Lane

First, skip this part if you understand probabilities.

For those of you who're still here, say you have a deck with 60 cards (who doesn't?), and that you are extremely unlucky. The only time your 4-digits hit first prize is the time you don't buy the ticket. Yes, THAT UNLUCKY. In Magic too.

Let's say you have a habit of drawing cards 1 by 1. And that you give up easily. If you don't draw a Force on your first draw, you'll give up. With 60 cards in your deck and only 4 Force of Will, there are 56 random cards that are not Force of Will. Of course you don't draw the FoW on the first draw. In math, the chances of you not drawing a FoW on the first draw is 56/60. Sad bloke, it's not easy to draw a Force on the first draw.

Let's do it again. Let's imagine that you're facing a 1st turn kill from a Belcher deck and have only 4 Force of Will to deal with it. So, you did what every man would – you played a 59 card deck with 4 FoW. Since you're smart and spiked the judge's drink with laxatives, no one will suspect you have an illegal deck. As you are a person that gives up if the first card you draw isn't a FoW, what are the chances of you NOT drawing a Force on the first draw in this case?

Simple, 59 cards, 4 FoW, 55/59 chances that you don't draw the Force. Still bad...

And this goes on. 58 cards gives a 54/58 chance of drawing a FoW on the first draw, 57 cards = 53/57, 56 cards 52/56 and so on and so forth...

Now comes the important part.

When you start the game by drawing 7 cards, you're just drawing 1 card at a time from a shrinking deck. You draw 1 card from a deck of 60, then another from a deck of 59, then a third from a deck of 58 and so on. This is exactly the same as what we imagined above.

So for 7 draws and no FoW, the probabilities combine in this way: 56/60 * 55/59 * 54/58 * 53/57 * 52/56 * 51/55 * 50/54. (You multiply the probabilities because the gods say so. Don't ask why, it's blasphemy. God does not play dice!) Copy and paste this into excel, and the chances of you not drawing a single Force of Will in your opening hand works out to be 0.600500374. You won't get a Force of Will in your opening hand 60% of the time.

Looking on the bright side, since the chances of not finding any Forces in your opening 7 is only 60%, that just means you'll find a Force of Will 40% of the time in your opening hand of 7.

Geek Alert

Those of you who skipped the previous section can come back now!

Now that you know why you'll draw at least 1 Force of Will 40% of the time, here comes the interesting part. You can calculate this in excel easily by using the Hypergeometric Distribution function, HYPGEOMDIST(a,b,c,d).

Hypergeometric Distribution Blah Blah Blah Blah

Before you ask any questions, open up excel and paste the stuff between the quotes in: “=HYPGEOMDIST(0,7,4,60)”.

Done that?

Did you get 0.600500374? Notice something? It's 60%, the same as the chances of not drawing any Force of Will in your opening 7!

Take a look closer at the formula: HYPGEOMDIST(0,7,4,60). See the 60 at the end? That's the number of cards in your library at the point you start drawing. 7 represents the starting hand, or the number of draws you're going to make. 4 means the number of Force of Will you can draw, and 0 means the number of times you draw a Force of Will. In English, the formula translates to this:
HYPGEOMDIST(0,7,4,60) gives me the chances of drawing 0 Force of Will in the next 7 draws, when I have 4 FoWs and 60 cards in my library.

Got it?

For those of you who are more mathematically inclined, you can find links for further reading at the end of this article.

But for those of you who care more about the application, you can use this to calculate the chances of you being manascrewed.

How to avoid being Manascrewed

Ever heard that you should play 17 lands in your SOM sealed deck prerelease/release party?

Ever wondered why?

Hypergeometric distribution holds the answer.

In a sealed deck, the mana curve is usually higher, with several cards around 3 or 4 cmc. In addition, we usually have 3-4 cards costing 5 or 6 mana that we want to cast when we do draw them. This means that we want to consistently get up to 5 mana without skipping a land drop in the first 5 turns. In math, this translates to the hypergeometric distribution function: HYPGEOMDIST(5,12,X,40).

Back to Earth, the function above in English simply means:
the chances of drawing 5 lands in the first 12 draws (opening hand of 7 + 5 turns down), using a deck of X lands and 40 cards.

When you plug the function into an excel sheet, you'll get this:



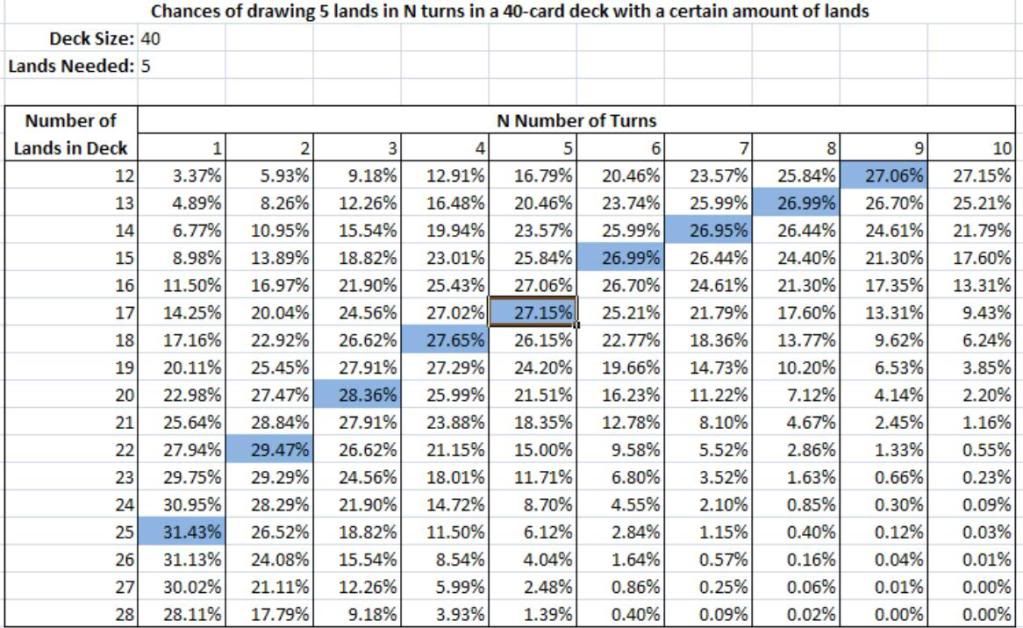
Looking at the picture, you'll find that the highlighted cells are those with the highest chances of achieving the goal of drawing 5 lands in N turns. Since we want to draw the lands in 5 turns, we look at the column of 5. The highest chance of drawing 5 lands happens to be 27.15%, and occurs when you have 17 lands in your deck. That is why the advice is to have 17 lands in your sealed deck.

How to avoid being Manascrewed in Constructed

When you change the excel sheet to reflect a deck of 60 cards, you get the table of probabilities for the constructed format.

For example: if you're playing a sligh deck, you'd want to consistently draw 2 lands in the first 2 turns. And maybe the third land in the 3rd to 5th turn. Plugging the numbers into the excel sheet gets you this:



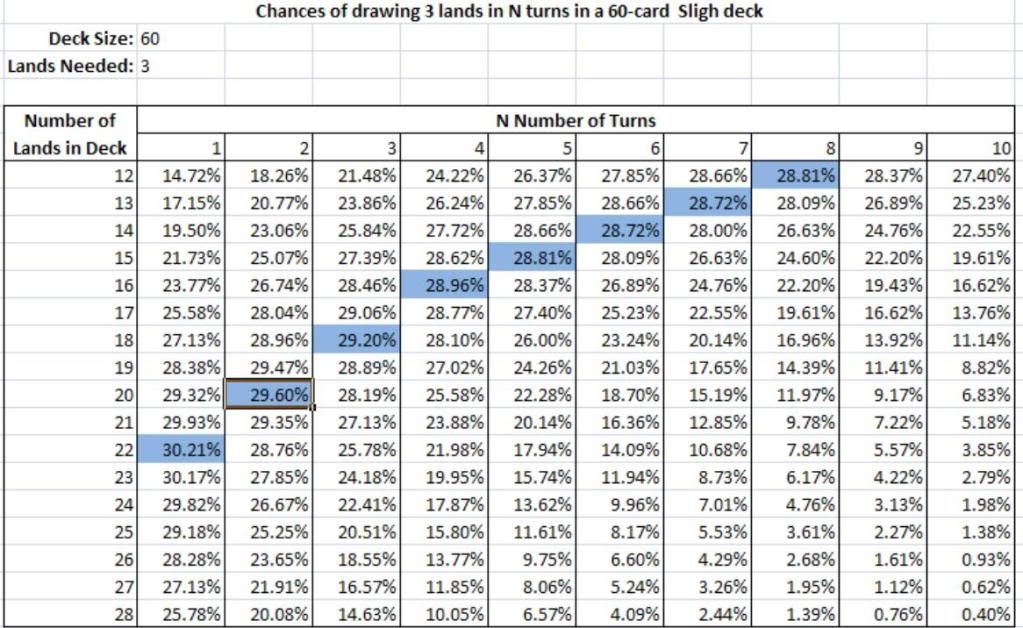
As you can see, the highest chances of getting 2 lands in the first 2 turns is 29.6%, when you have 20 lands. That is why players recommend the 20-20-20 rule for a sligh deck. 20 lands, 20 creatures, 20 burn.

Bonus!

Just for you readers out there, I've made the excel sheet I've used in the examples above accessible for here. Just click here to see it. Note: you need to log in to play around with the excel sheet.

Other Applications

When you get to master probabilities, you can calculate the chances of opening a hand with a certain combination of cards. For example, you can calculate and see the chances of getting a hand with 2 Mox Diamond, 2 Lands, 1 Ancient Tomb/City of Traitors, 1 Smokestack, and 1 random. You can compare it with the chances of opening a hand of 1 Mox Diamond, 1 Land, 1 Ancient Tomb/City of Traitors, 1 Trinisphere, and 3 random and see which is more probable.

However, that is perhaps better left for another time, after I've mastered secondary school math...

Further Reading

Wikipedia is your best friend
MTG The Source discussion and many many opinions: How many blue cards are needed to support Force of Will
The math in Magic The Gathering
Why fetchlands dun thin your deck as much as you want to

I'm reading: The 40% Rule (or why you don't draw that FoW) Tweet this!